CALCUL INFINITÉSIMAL - Calcul à plusieurs variables

CALCUL INFINITÉSIMAL - Calcul à plusieurs variables

Le calcul infinitésimal des fonctions de plusieurs variables a eu un développement plus tardif que celui des fonctions d’un seul argument. Inauguré avec un siècle de retard, il ne parvient à établir solidement ses fondements qu’au début du XX^e siècle.

Ce n’est qu’aux environs de 1930 que sont abordés les problèmes difficiles de cette branche de l’analyse, très utilisée depuis lors.

1. La préhistoire

Le formalisme des dérivées partielles

Avant d’étudier le comportement d’une fonction f (x ,y ) de deux variables, lorsque x et y varient simultanément et indépendamment , on commence par faire varier x et y successivement. Fixons la valeur de y : la dérivée de la fonction x 料 f (x ,y ), lorsqu’elle existe, s’appelle la dérivée partielle 煉f / 煉x (x ,y ) de f par rapport à x (à y constant). La notation utilisant le 煉 pour désigner la dérivation partielle, par opposition au d désignant la dérivation ordinaire, a été préconisée par Legendre (1786) et vulgarisée par Jacobi (1841). Si, maintenant, on fait varier x et y en fonction d’une même variable t , on trouve que:

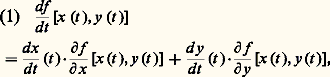ce qui fait apparaître les dérivées partielles de f comme des intermédiaires de calcul commodes.

Les dérivées partielles apparaissent, en 1755, dans le traité Institutiones calculi differentialis d’Euler, et, en 1747, chez A. Clairaut. Ils y ont reconnu l’outil de base du calcul différentiel à plusieurs variables. Malheureusement, cette notion est essentiellement liée au choix d’un système de coordonnées.

Par exemple, considérons les formules W = RI² = EI = E²/R, qui traduisent un cas particulier des lois d’Ohm en électricité. On constate que le symbole 煉W/ 煉I est égal à 2 RI, E ou 0 selon l’expression de W que l’on adopte. L’explication de ce paradoxe vient de ce que la dérivation par rapport à I n’a pas la même signification selon que l’on opère à R constant (et E variable), ou à E constant (et R variable) et enfin si l’on fixe E et R.

S’inspirant de ce que Leibniz avait fait pour la différentielle des fonctions d’une variable, Euler et Clairaut étudièrent une expression remarquable, la différentielle totale :

c’est une fonction de quatre variables indépendantes x ,y ,dx ,dy (linéaire par rapport aux deux dernières). Cette expression possède un caractère invariant lorsqu’on la soumet à des changements de variables du type particulier suivant: si l’on exprime x et y en fonction de nouvelles variables X,Y au moyen des formules x = x (X,Y), y = y (X,Y), et si l’on effectue, en même temps , le changement de variables «covariant», selon les formules:

on constate que la différentielle totale de f prend la même forme (2) que l’on exprime df à l’aide de x ,y ,dx et dy ou à l’aide de X,Y, d X et d Y.

Les dérivées partielles sont susceptibles d’être dérivées partiellement à leur tour. On obtient ainsi les dérivées partielles secondes: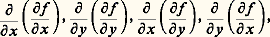

que Jacobi note respectivement:

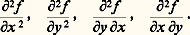Euler et Clairaut avaient déjà constaté que le résultat ne dépend pas de l’ordre dans lequel on effectue les dérivations (pour autant que ces auteurs n’opéraient tacitement que sur de «bonnes fonctions», c’est-à-dire des fonctions que nous nommons aujourd’hui analytiques), soit:

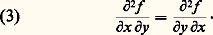À titre de preuve, Euler se borne à invoquer la symétrie de l’expression:

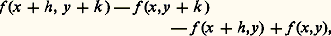et Clairaut opère formellement sur un développement en série.

Une combinaison linéaire à coefficients complexes de dérivations partielles s’appelle un opérateur différentiel linéaire à coefficients constants (par exemple:

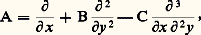où A, B, C sont des nombres complexes). Ces opérateurs sont susceptibles d’être ajoutés et composés entre eux: il en résulte une structure algébrique sur l’ensemble des opérateurs différentiels à coefficients constants qu’en langage moderne on peut formuler ainsi: «L’ensemble des opérateurs différentiels à coefficients complexes opérant sur des fonctions de deux variables est un anneau (pour l’addition et la composition), isomorphe à l’anneau des polynômes C [X,Y] à deux indéterminées X et Y.» (Par exemple, à l’opérateur cité ci-dessus correspond le polynôme AX + BY² 漣 CXY².) L’isomorphisme précédent s’explique par l’analogie complète qui existe entre les règles de calcul qui régissent l’addition et la multiplication des polynômes d’une part, l’addition et la composition des opérateurs différentiels à coefficients constants d’autre part. Parmi ces règles, la formule (3) exprime la commutativité des dérivations partielles. Mais, au XVIII^e siècle, de telles explications ne pouvaient être pleinement comprises: les calculateurs imaginaient une profusion de règles de calcul «symboliques», dont l’efficacité restait mystérieuse.

Voici une application des considérations précédentes. En tenant compte de l’isomorphisme précité, on peut développer l’opérateur (face=F0019 煉/ 煉x + 煉/ 煉y ) itéré n fois, grâce à la formule du binôme de Newton:

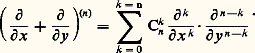En appliquant les deux membres à la fonction f (x )g (y ) et en remplaçant y par x dans le résultat, on aboutit à la formule de Leibniz:

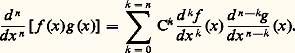La théorie des équations aux dérivées partielles oblige à manipuler de plus en plus des expressions différentielles: l’importance du laplacien: face=F0019 煉²/ 煉x ² + 煉²/ 煉y ² provient du fait que c’est (à un coefficient près) le seul opérateur différentiel à coefficients constants, homogène du second ordre, qui soit invariant par rotation des axes. Le laplacien, à cause de cette signification intrinsèque, apparaît dans de nombreux phénomènes physiques.

L’étude de certaines équations aux dérivées partielles liées à des problèmes de géométrie différentielle a conduit à adopter les notations de Monge:

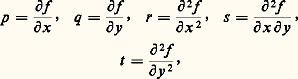utilisées à la fin du XIX^e siècle, mais qui sont tombées en désuétude, faute de pouvoir se généraliser aux cas des fonctions de n variables, et à valeurs vectorielles.

Euler s’est également occupé du calcul des dérivées d’une fonction implicite : partant d’une équation f (x,y ) = 0, il suppose, sans trop de scrupules, que l’on peut trouver une fonction x 料 y (x ) satisfaisant à f [x,y (x )] 令 0. Il calcule alors la dérivée y (x ) à partir de l’équation:

et en déduit l’expression des dérivées successives de y.

Étudiant de la même façon la résolution d’un système: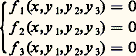

Jacobi introduit la notion de déterminant fonctionnel (appelé aussi déterminant jacobien) défini par:

et dégage les règles du calcul formel qui le régissent. Il met en évidence la notion de dépendance fonctionnelle analogue à la dépendance linéaire entre formes linéaires.

Au XIX^e siècle commence l’étude algébrique des opérateurs différentiels linéaires à coefficients variables: deux tels opérateurs ne commutent pas nécessairement (on s’en convaincra en composant les opérateurs d /dx et x (d /dx ) relatifs à des fonctions d’une seule variable). On introduit alors diverses expressions différentielles (déterminants hessiens ou wronskiens, crochets de Lie, parenthèses de Poisson, invariants intégraux, etc., qui préparent la voie au calcul différentiel extérieur, à l’analyse tensorielle et à la géométrie différentielle moderne (cf. GÉOMÉTRIE DIFFÉRENTIELLE CLASSIQUE, VARIÉTÉS DIFFÉRENTIABLES). L’aboutissement de cet effort d’algébrisation sera l’édification d’une science traitant abstraitement des objets mathématiques soumis aux mêmes règles de calcul que les opérateurs différentiels: l’algèbre différentielle ainsi édifiée s’affranchit de toutes considérations de continuité et de limite, et trouve des applications dans l’étude des fonctions définies sur un corps quelconque et jusqu’en arithmétique.

En ce qui concerne les notations, un perfectionnement important a été apporté, en 1934, par H. Whitney, qui a introduit l’usage des multi-indices. Un multi-indice à n variables est un système ordonné de n entiers ( 見¹, 見², ..., 見ⁿ ), que l’on désigne par un seul symbole 見. Dans ces conditions, on écrit: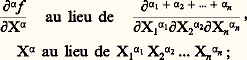

on pose, de plus:

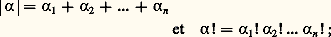avec de telles notations, la série de Taylor s’écrit alors comme une série à une variable, mais avec une sommation étendue à l’ensemble de tous les multi-indices:

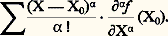Formulation intrinsèque de la théorie

Les inconvénients des dérivées partielles posèrent, dès l’apparition du calcul vectoriel, le problème de la formulation intrinsèque de la théorie, en mettant en évidence des expressions invariantes par changement de coordonnées; M étant un point de coordonnées (x,y,z, ... ), on ne parlera plus de fonctions des variables, mais de fonctions du point M.

Une étape historique importante, aujourd’hui complètement dépassée, a été l’élaboration, par O. Heaviside et W. Gibbs, de l’analyse vectorielle, qui met l’accent sur certaines expressions invariantes par changement de coordonnées rectangulaires dans l’espace à trois dimensions. La structure euclidienne y joue donc un rôle primordial. À une fonction numérique Mf (M) = f (x ,y ,z ) (où x, y, z sont les coordonnées de M par rapport à une base orthonormée), on associe le vecteur, dont les composantes sont:

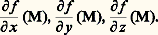C’est le gradient de la fonction f. Il est lié à la différentielle totale de f par la formule:

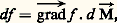où le second membre représente un produit scalaire et d ぬ le vecteur dont les composantes sont dx, dy, dz . À un champ de vecteur M 料 ふ (M), défini par les trois composantes X(M), Y(M), Z(M) du vecteur ふ, on associe une fonction scalaire, la divergence du champ:

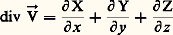et une fonction vectorielle, le rotationnel de ふ, dont les composantes sont:

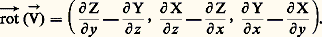Le gradient, la divergence et le rotationnel sont des notions invariantes par changement d’axes orthonormés et sont soumises à un grand nombre de règles de calcul «symboliques», dont les plus simples sont:

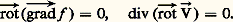Ces notions permettent d’écrire, sous une forme concise et suggestive, un grand nombre de formules de la physique théorique, de la mécanique et de la géométrie. Par exemple, les divers cas particuliers de la formule de Stokes (attribués à Green, Ampère, Ostrogradsky, etc.) prennent la forme:

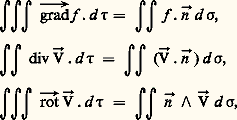où d 精 (resp. d 靖) désigne l’élément de volume (resp. d’aire), où l’intégrale triple est étendue à un domaine tridimensionnel orienté, et où l’intégrale de surface est étendue au bord orienté dans ce domaine, ょ représente le vecteur normal à la surface considérée.

Mais cette analyse vectorielle ne couvre pas l’ensemble de tous les besoins de la physique mathématique. Elle ne déborde pas le cadre des fonctions de trois variables et des changements de bases orthonormales. La véritable solution du problème de la formulation intrinsèque du calcul différentiel n’a été obtenue qu’après l’édification de l’analyse tensorielle (par Ricci et Levi-Civita) et du calcul différentiel extérieur (par Élie Cartan). Bien que ces théories n’aient été exposées à l’origine qu’en termes de coordonnées, il n’a pas été difficile (après la construction axiomatique de l’algèbre linéaire et multilinéaire), de les traduire en langage intrinsèque.

Le calcul différentiel extérieur explique l’origine (qui paraissait quelque peu mystérieuse) des notions de gradient, de rotationnel et de divergence, puisque les dérivées extérieures de:

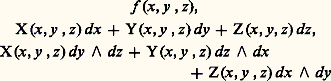sont respectivement:

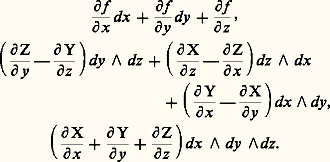La formule de Stokes qui s’exprimait, nous l’avons vu, sous des formes très diverses et d’emploi limité dans le langage de l’analyse vectorielle s’écrit aujourd’hui:

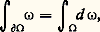où 諸 est une forme différentielle, d 諸 sa différentielle extérieure, 行 une chaîne orientée (cf. TOPOLOGIE – Topologie algébrique), et 煉 行 le bord orienté de 行.

Les progrès de l’algèbre linéaire ont permis enfin de définir la différentielle sans aucun recours aux coordonnées sous une forme qui s’applique également aux fonctions définies sur des espaces de dimension infinie (cf. chap. 2).

Après que R. Gateaux et V. Volterra aient dégagé la notion de dérivée directionnelle d’une fonction définie sur un espace fonctionnel (établissant ainsi la synthèse entre le calcul des variations (cf. calcul des VARIATIONS) et le calcul différentiel classique, O. Stoltz et M. Fréchet donnaient la définition intrinsèque de la notion de différentielle. Ces travaux ont fait prendre conscience du fait fondamental suivant: pour traiter le calcul différentiel des fonctions définies sur un espace vectoriel normé E et prenant leurs valeurs dans un espace normé F, il est indispensable de manier simultanément de nombreux espaces auxiliaires obtenus à partir de produits tensoriels des espaces E, F et du dual de E. En particulier, chacune des dérivées successives d’une application différentiable f doit prendre ses valeurs dans un espace différent.

Cette conception oblige à manipuler simultanément un grand nombre d’espaces normés, ayant des dimensions différentes, ce qui n’est pas fait pour faciliter l’intuition géométrique. Pour obvier à cet inconvénient, C. Ehresmann a créé, en 1943 et en 1952, deux outils extrêmement commodes: la notion d’espace fibré et la notion de variété des jets. Grâce à ce langage, on peut concevoir le support géométrique du calcul différentiel à n variables comme un domaine 行 de l’espace à n dimensions, et, «au-dessus» de chaque point M de 行, on imagine une «fibre», formée par une collection d’objets mathématiques (vecteurs, tenseurs, matrices, covecteurs et cotenseurs, etc.), dont on aura besoin pour décrire la théorie. La description a priori de la variété des jets, exprimée de façon intrinsèque, permet de s’affranchir de la manipulation de signes hérissés d’indices compliqués et d’utiliser à nouveau un langage géométrique.

Apparition de la rigueur

Le flux de formalisme qui caractérise la première époque du calcul infinitésimal fut suivi par un reflux critique dans le domaine de la rigueur.

Sous l’influence de Cauchy, Abel et Weierstrass, on se préoccupa de reprendre les principales formules découvertes plus ou moins empiriquement au siècle précédent, pour en préciser au mieux les limites de validité. Ainsi, H. A. Schwarz prouva, en 1873, que la formule:

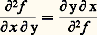est valable, sous réserve de la continuité d’un des deux membres par rapport à l’ensemble des variables. Peano donna l’exemple de la fonction:

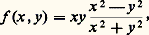prolongée par continuité en posant f (0,0) = 0, pour laquelle la permutation des dérivées partielles n’est pas licite.

Peano entreprit systématiquement de dépister les affirmations non rigoureuses, largement répandues à l’époque, construisit des contre-exemples, aujourd’hui classiques, et tenta de redémontrer certains théorèmes, sous les hypothèses les plus faibles possibles. C’est ainsi qu’il améliora l’exposition du théorème des accroissements finis et démontra la formule de Taylor (cf. chap. 2), pour les fonctions d’une ou plusieurs variables, en éliminant toute hypothèse superflue; on lui doit en outre la formule classique sur le reste de Young (trouvée par Peano avant cet auteur). Il signala une erreur célèbre touchant les maxima (ou minima) des fonctions: on pensait que l’inspection des termes de plus bas degré du développement de Taylor, au voisinage de l’origine d’une fonction, ainsi que le comportement de cette fonction sur chaque droite passant par l’origine permettait de décider de l’existence d’un extrémum en ce point. Or la fonction (y 漣 x ²)(y 漣 2 x ²), pour laquelle le terme de plus bas degré est y ², admet un minimum relatif nul sur chaque droite passant par l’origine; cependant, elle prend des valeurs négatives dans tout voisinage de l’origine.

Vers la même époque paraissent, dans les traités d’analyse, les premières démonstrations correctes du théorème des fonctions implicites et de quelques-unes de ses variantes. La préhistoire prend fin, le véritable développement commencera trente ans plus tard.

2. Exposé moderne de la théorie élémentaire

Dérivée première

Soit E et F deux espaces normés, et 行 un ensemble ouvert de E: on dit que deux fonctions continues f et g (définies sur 行 et à valeurs dans F) admettent un contact d’ordre r (où r est un nombre entier) au point A 捻 行 si le rapport:

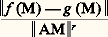tend vers 0 lorsque M tend vers A. En particulier, lorsque r = 1 on dit que f et g sont tangentes au point A; cette définition implique que f (A) = g (A).

Une fonction continue f (définie sur 行 et à valeurs dans F) est dérivable en A 捻 行, s’il existe une fonction continue affine:

(où L est une application linéaire continue de E dans F, c’est-à-dire un élément de face=F9796 L(E,F) qui est tangente à f au point A). L s’appelle aujourd’hui la dérivée de f au point A (dans l’ancienne terminologie, c’était la « différentielle au sens de Stolz-Fréchet » ou plus brièvement la différentielle de f au point A). On la note d’ordinaire D¹f (A). Lorsque f est dérivable en tout point de 行, la fonction dérivée est l’application A 料 D¹f (A) définie dans 行 et à valeurs dans face=F9796 L(E,F). On dit que f est continûment dérivable (ou encore de classe C¹) si la fonction dérivée est continue, lorsqu’on munit face=F9796 L(E,F) de sa norme usuelle: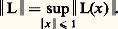

Dans le cas particulier où E = Rⁿ et F = R, toute fonction de classe C¹ admet des dérivées partielles continues et la dérivée de f au point de coordonnées (x ¹, x ², ..., x ⁿ ) est la forme linéaire qui associe au vecteur de coordonnées (dx ¹, dx ², ..., dx ⁿ ) le nombre:

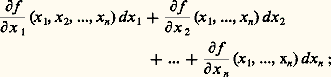la dérivée coïncide donc avec la «différentielle totale» d’Euler (cf. chap. 1).

Lorsque E = Rⁿ et F = R^p la fonction f est définie par p fonctions numériques f ¹, f ²,..., f ^p . La dérivée de f en un point de coordonnées (x ¹, x ², ..., x ⁿ ) est, lorsqu’elle existe, l’application linéaire appartenant à face=F9796 L(Rⁿ , R^p ) définie par la matrice jacobienne des fonctions f ^j (j 諒 p ) par rapport aux variables x ⁱ (i 諒 n ).

Une fonction qui possède des dérivées partielles en chaque point de 行 n’est pas nécessairement dérivable, comme le montre l’exemple de la fonction scalaire:

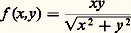(prolongée par f (0, 0) = 0). Son graphe est un demi-cône dont le sommet est à l’origine; il ne possède donc pas de plan tangent en ce point. Par contre, on montre que toute fonction qui admet des dérivées partielles continues par rapport à l’ensemble des variables est nécessairement dérivable.

Dérivées successives

Supposons que la fonction dérivée M 料 D¹f (M) soit elle-même dérivable: sa dérivée D¹(D¹f )(M) appartient à face=F9796 L[E, face=F9796 L(E,F)]. On peut l’identifier à une application bilinéaire continue de E 憐 E dans F, et dans ce cas on l’appelle la dérivée seconde de f au point M et on la note D²f (M). On peut ainsi définir les dérivées successives de proche en proche.

On peut également donner une définition directe des fonctions r fois continûment dérivables (ou de classe C^r ) en utilisant la notion de polynôme défini sur E et à valeurs dans F. Désignons par face=F9796 L^k (E,F) l’espace vectpriel des applications continues k -linéaires, symétriques, définies sur (E)^k et à valeurs dans F. En d’autres termes L^k 捻 face=F9796 L^k (E, F) est une application:

séparément linéaire par rapport à chaque argument, invariante lorsqu’on permute arbitrairement les vecteurs Vⁱ entre eux, et telle que 瑩L^k [ ふ¹, ふ², ..., ふ^k ] 瑩^F reste borné lorsque les vecteurs ふⁱ restent tous dans la boule unité de E. Un monôme de degré k défini dans E et à valeurs dans F est alors par définition une fonction de point:

remarquons que lorsque E est de dimension finie et que l’on exprime のM à l’aide de ses composantes, on n’obtient pas un monôme ordinaire, mais un polynôme homogène de degré k ayant pour coefficients des vecteurs de F. Un polynôme sur E et à valeurs dans F est maintenant, par définition, une somme finie de monômes.

Une formule de Taylor permet de remplacer les vecteurs のM qui interviennent dans la définition précédente par des vecteurs だM où A 捻 E. On dira qu’une fonction f , définie sur 行, admet un développement limité d’ordre m au point A, s’il existe des L^k 捻 face=F9796 L^k (E, F), k = 1,2, ..., n , tels que le polynôme:

satisfasse à la condition: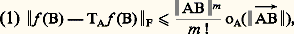

où la fonction o^A tend vers 0 lorsque 瑩 だB 瑩 tend vers 0.

Si un tel «polynôme de Taylor» existe en tout point A 捻 行, si les «coefficients» k !L^k (que l’on note plutôt D^k f (A) et que l’on appelle les dérivées k-ièmes de f ) varient continûment sur 行, et s’il existe en chaque point A 捻 行 une fonction 礼^A satisfaisant à la condition (1) on dit que f est de classe C^m dans 行 (ou encore m fois continûment dérivable). Il est possible alors de transposer au cas des fonctions définies sur 行 la plupart des formules à une variable. Par exemple, si f est de classe C^{m + 1} , le reste de son développement d’ordre m , qui s’écrit, dans le cas d’une variable:

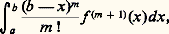s’exprime ici par:

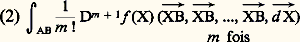où l’intégrale curviligne est prise le long de n’importe quelle courbe rectifiable joignant A à B dans 行.

L’expression (2), appelée reste intégral de la formule de Taylor, donne la valeur exacte de f (B) 漣 ^Af (B). On utilise aussi diverses majorations de ce reste. Si la dérivée AD^Am f est une fonction uniformément continue dans 行, on peut majorer le reste par une expression de la forme:

où 諸 (x ) est une fonction continue qui tend vers 0, lorsque x tend vers 0 (majoration de Young ).

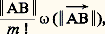Le théorème des fonctions implicites et ses variantes

Étant donné deux domaines 行 說 E (resp. 行¹ 說 E¹), rappelons qu’une application f de 行 sur 行¹ est un homéomorphisme si f est bijective, continue ainsi que l’application réciproque f ^-1. Un homéomorphisme peut être de classe C^m mais on dit que c’est un difféomorphisme (de classe C^m ) si l’application réciproque f ^-1 est également de classe C^m (et l’on montre qu’il suffit pour cela que f ^-1 soit de classe C¹). L’exemple de l’application t 料 t ³ de R sur R montre qu’un homéomorphisme de classe C¹ n’est pas nécessairement un difféomorphisme.

Théorème d’inversion locale. E et F étant deux espaces de Banach (c’est-à-dire des espaces normés complets ), soit f une application de classe C^m définie dans un voisinage du point A 捻 E et prenant ses valeurs dans F. Si la dérivée D¹f (A) est un isomorphisme linéaire de E sur F, alors il existe un voisinage U de A dans E et un voisinage U¹ de f (A) dans F, tel que la restriction de f à U soit un difféomorphisme sur U¹.

Commentons cet énoncé. Une fonction différentiable f est «approximativement» égale au voisinage de A à sa dérivée D¹f (A). Le théorème précédent exprime que si l’application linéaire tangente en A est inversible alors f est lui-même inversible au voisinage de A. Ainsi le comportement de la dérivée en un point conditionne le comportement local de f dans tout un voisinage de A.

Le théorème précédent s’applique, par exemple, à l’application de R² dans R² définie par X = e ^x cos y , Y = e ^x sin y (inspirée par l’application z 料 e ^z de C dans C). On notera que cette application n’est pas globalement bijective.

Théorèmes de submersion et d’immersion locale. Si l’un au moins des espaces de Banach E et F est de dimension finie, soit f une application de classe C^m , définie dans un voisinage de A 捻 E. Si la dérivée D¹f (A) est surjective (resp. injective ), alors il existe un voisinage U de A dans E et un voisinage U¹ de f (A) dans F, et enfin un difféomorphisme de U sur U (resp. un difféomorphisme ¹ de U¹ sur U¹) tel que f ⁰ (resp. ^{1 0} f ) soit la restriction à U d’une application linéaire surjective (resp. injective) de E dans F.

Ces théorèmes signifient que, si une application f est «approximativement» une application linéaire surjective (resp. injective), on peut la transmuer en une application linéaire du même type. La restriction sur la dimension finie d’un des espaces n’est pas indispensable, mais il faut ajouter une hypothèse supplémentaire pour que les énoncés précédents restent valables.

Forme archaïque du théorème de submersion locale (théorème des fonctions implicites ). Si p fonctions:

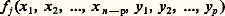(où j = 1, 2, ..., p ) sont de classe C^m et si le déterminant jacobien des fonctions f ^j par rapport aux variables y ^j ne s’annule pas à l’origine, on peut exprimer localement les y ^j comme fonctions de classe C^m des variables X = (x ¹, x ², ..., x ^n-p ) de façon à satisfaire au système d’équations «implicites»:

(où j = 1, 2, ..., p ).

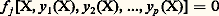Il existe une autre variante de ces théorèmes, appelée théorème du rang constant , relative au cas où la dérivée de l’application f garde un rang constant au voisinage de l’origine.

Les «images» et «noyaux» des applications différentiables satisfaisant aux énoncés précédents sont localement des morceaux de «variétés différentiables» ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]}, qui devront être convenablement recollés pour aboutir à une théorie globale.

Un théorème beaucoup plus fin, démontré par J. Nash (1956), concerne le cas où D^A1 f , sans être surjective, a une image partout dense dans l’espace de Banach F, de dimension infinie. Dans ces conditions, la résolution locale du système d’équations implicites ne peut s’obtenir qu’au prix d’une certaine perte de dérivabilité.

3. La théorie fine contemporaine

L’œuvre de H. Whitney

Le mathématicien américain Hassler Whitney, dont la contribution à des branches très variées des mathématiques a été souvent décisive (théorie des graphes, topologie algébrique et différentielle, axiomatisation de la notion de variété ou de produit tensoriel, étude des ensembles analytiques réels, etc.), est le véritable initiateur du renouveau du calcul différentiel des fonctions de plusieurs variables. Parmi ses contributions, citons:

Le théorème du prolongement (1934). En chaque point d’un ensemble fermé F quelconque de Rⁿ on se donne un polynôme à n variables de degré inférieur ou égal à m. Whitney énonce une condition nécessaire et suffisante pour qu’un tel champ de polynômes soit la restriction à F du champ des polynômes de Taylor d’une fonction f de classe C^m . Ce théorème permet, en particulier, de construire des fonctions f de classe C^m ayant certaines singularités données à l’avance: on commence par se donner l’ensemble F des points singuliers puis l’on cherche à prolonger un champ de polynômes défini sur F. Indiquons que ce théorème est encore valable pour m = 秊. Un cas particulier très important est celui où F se réduit à un seul point; on obtient le théorème d’É. Borel généralisé à n variables : «Il existe une fonction f de classe C size=1^秊 dont les dérivées partielles prennent en un point donné des valeurs arbitrairement choisies.» En d’autres termes, la série de Taylor d’une fonction de classe C size=1^秊 peut être n’importe quelle série formelle .

Caractérisation des idéaux fermés de fonctions différentiables . L’ensemble des fonctions numériques de classe C^m définies sur un pavé compact K constitue une algèbre de Banach (lorsque m est fini) pour la norme de la convergence uniforme d’ordre m (c’est-à-dire de la convergence uniforme de chacune des dérivées partielles). La structure des idéaux de cette algèbre est d’une grande complexité, mais H. Whitney a démontré, en 1944, le théorème suivant concernant les idéaux fermés.

Théorème. Pourqu’une fonction f de classe C^m sur K appartienne à un idéal fermé 溜, il faut et il suffit qu’à chaque point de K on puisse associer une fonction g ^A 捻 溜 telle que f et g ^A aient les mêmes polynômes de Taylor en A. Ce théorème signifie que l’appartenance ponctuelle à 溜 implique l’appartenance globale .

Classification des singularités

En 1925, le mathématicien américain Marston Morse a inauguré l’étude des singularités des fonctions de classe C^m en montrant que l’on pouvait approcher toute fonction numérique f de classe C^m à n variables par des fonctions dont les seuls points singuliers sont des points isolés critiques (c’est-à-dire dont la dérivée s’annule) dont la dérivée seconde est une forme bilinéaire associée à une forme quadratique non dégénérée. Il montra en outre qu’il était possible de transmuer un tel point singulier, à l’aide d’un difféomorphisme local, en une fonction qui est une somme algébrique des carrés des coordonnées.

Ainsi, on abandonne l’étude inextricable de toutes les singularités possibles pour ne s’intéresser qu’à des singularités génériques auxquelles on peut toujours se ramener grâce à une approximation et à une transmutation.

En 1955, H. Whitney résoud la même question concernant les applications du plan R² sur le plan R². Il met en évidence deux singularités génériques: le pli qui se ramène au modèle (x,y ) 料 (x ²,y ) et la fronce dont le modèle est (x,y ) 料 (x ³ 漣 3 xy, y ). Dans ces travaux, un rôle essentiel est joué par le théorème d’A. Sard (1942), dont le cas particulier simple relatif aux fonctions C size=1^秊 avait déjà été démontré par Morse:

Théorème . Étant donné une application de classe C^m de Rⁿ dans R^p la mesure au sens de Lebesgue de l’image des points singuliers est nulle lorsque m 閭 n 漣 p + 1 (Whitney a construit un exemple montrant que cette inégalité est nécessaire).

Utilisant ce résultat, R. Thom a démontré un théorème de transversalité qui, généralisant la méthode de Morse, indique dans quelle condition une application f de Rⁿ dans R^p peut être approchée par des fonctions n’ayant que des singularités dûment cataloguées.

Les cas p =2n +1, p =2n et p =2n 漣1, entièrement élucidés par Whitney, constituent son célèbre théorème du plongement selon lequel toute variété différentiable à n dimensions ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]} abstraite, peut être réalisée comme sous-ensemble d’un espace R²ⁿ . On peut même se contenter d’un espace R^2n-1 si l’on accepte de laisser subsister des «self-intersection». Par exemple, la «bouteille de Klein» peut être réalisée dans R³ à condition de se traverser elle-même, et dans R⁴ sans aucun point double.

Étude des idéaux de fonctions différentiables

À la suite du théorème de H. Whitney, déjà cité, S. Lojasiewicz a démontré en 1959 que tout idéal engendré dans l’algèbre des fonctions C size=1^秊 par une fonction analytique réelle est nécessairement fermé.

Ce théorème signifie qu’une fonction f de classe C size=1^秊 est divisible par une fonction analytique g , si la division «ponctuelle» des séries formelles de Taylor en chaque point du domaine de f et g est possible.

En 1962, B. Malgrange est parvenu à démontrer que le théorème de préparation de Weierstrass, classique dans le cas des fonctions analytiques de plusieurs variables ^{[cf. FONCTIONS ANALYTIQUES]} reste valable pour les fonctions C size=1^秊.

Il s’agit d’une division avec reste (analogue à la division euclidienne): il est possible de diviser au voisinage de l’origine une fonction C size=1^秊 de n + 1 variables (y , X) = (y , x ¹, x ², ..., x ⁿ ) par un polynôme:

Ici les a ⁱ sont des fonctions C size=1^秊 qui s’annulent pour X = 0, avec un reste qui est un polynôme de degré inférieur à k en y , dont les coefficients sont C size=1^秊 en X.

Dans le cas analytique, on sait qu’une telle division s’effectue de façon unique. Il n’en est plus de même dans le cas C size=1^秊, ce qui fait la difficulté du théorème de Malgrange.

Encyclopédie Universelle. 2012.